尤涅若的小宇宙的视频 · 162 播放主要参考的学习资料是：机器人动力学讲义Robot Dynamics Lecture Notes与论文Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control。本人先从讲义中学到了一部分机器人的基础知识，但是也只是学到一点皮毛，对笛卡尔坐标变换和变分法等概念依旧一无所知，有待后续学习。利用所学皮毛对论文进行初步的理解如下。与Cheetah 2完全依赖MPC的控制策略不同，Cheetah 3与mini Cheetah首先利用MPC求出机器人当前最佳受力（即地面对机器人产生的弹力），这一过程由于计算复杂度的原因耗时较长，然后利用WBC从得到的地面反作用力，计算出多任务优先级不同情况下机器人各关节扭矩、位置和速度。为了将MPC过程得到的最优地面反作用力与WBC全身控制算法结合，文章使用了Whole Body Impulse Control(WBIC)控制策略，这种控制方式与现有的全身控制策略并无太大差异，主要的特点是该策略针对四足机器人的浮动基特征下，利用受到地面反作用力进行全身关节控制，而不是传统WBC中利用当前位姿进行全身控制。WBC与MPC结合进行凸优化的效果优于一般的MPC控制策略，有效避免了陷入局部极小的困境。关于convex MPC问题这篇文章没有细讲，将在未来学习过程中进行补充。混合控制体系结构文章方法的核心思想是将控制分为两个简单的控制单元，以减轻控制的复杂程度。首先是使用MPC与以下简单的质心力学公式：
其中p即position属机器人的质心位置，fi为地面的反作用力，nc为控制器的数量，cg为引力项，I为机器人各关节转动惯量张量，w为角速度，ri为受力的动力臂。第二个控制体系将注意力放在各运动关节的高频反馈控制，不再使用简单的质心公式。
A为广义质量矩阵，qf为floating base的位置，qj为为各个joint的位置，b与g分别为科里奥利力项和引力项，t为关节力矩，Jc为反作用力受力位置的连接雅克比矩阵，fr为输入量反作用力。参考机器人动力学教材71页的浮动基机器人动力系统的表述，A，b与g都是关于运动位姿的函数，MIT使用了基于卡尔曼滤波的状态估计器和自定义动力学引擎对运动状态进行计算。
机器人动力学教材中关于浮动基机器人动力学公式的说明模型预测控制文章只考虑机器人进行航向角变化的简单情况，机器人身体角加速度和全局惯性张量的计算公式分别为：
Rz是将局部（基座）惯性张量映射到全局惯性张量的投影，根据假设只是关于航向角的函数。同时由于控制时采用高带宽控制，假设机器人当前位姿接近目标位姿，对当前位姿I进行线性化（泰勒展开），又由于假设滚动角和俯仰角约等于0，I接近单位矩阵，得到如下结果：
结合以上四个公式得到离散化的控制规律：
字有点丑得到模块化的控制策略：
控制量包括机器人转向，位置，关节角速度与位置速度。最后转化为QP求最小跟踪误差下的反作用力：
QR为权重矩阵WBC全身控制在讲述WBIC之前先简单讲述一下WBC的概念。给出一个运动学背景的推导过程：机械臂终端速度we由机械臂关节转角q及其导数所决定，之间关系由简单映射雅克比矩阵决定：
在控制问题中我们对逆运动学问题更感兴趣：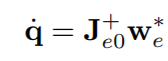
其中Je0伪逆的解通常是不唯一的，取决于该矩阵的性质。当Je0的秩小于n时，这种配置被称为redundancy（冗余）。系统中的冗余意味着存在无穷多个解
矩阵N为Je0的null-space projection matrix（空投影矩阵），满足Je0N=0。在这种情况下允许使用任意的q0带入计算而影响q导数的结果，但并不改变固定目标we。
利用这个理论基础，对具有不同优先级的多任务控制系统进行分析。假设当前任务具有递减的优先级：
递减优先级的意义在于首先应满足当前任务要求，即本例中的终端速度w1=we。J1即为Je0。同时，控制中对某些关节的速度有要求w2，J2为机械臂关节转角速度到w2的投影：
注意此时完全符合上式任务要求 且
。解出q0导数：
反代入原式，得到：
上面是2个任务情况下的控制规律，在task=nt情况下的迭代结果为：
这个迭代结果我还不是很理解，在这里mark一下希望有人可以教我。当有3个任务时应该怎样计算？是拆解N1q0’项进行计算吗？其中
在多任务空间的动力学中也有相似的结果：
注意这里的区别在于we的二阶导数存在两项：
以上阐明WBC的基本概念：利用关节雅克比矩阵非满秩情况下伪逆的性质，对冗余部分进行第二次规划，以达到对关节部位的任务要求。WBIC全身脉冲控制然后下面讲述对文章中WBIC方法的个人理解。用q表示整个机器人全配置空间的向量，其中qf代表身体转向，qj代表所有关节的角度。
首先写出如下方程，其中ei代表位置关于期望的偏差，在i（任务数量）=1时，该偏差就等于机器人全配置空间变化量的连接投影。当处于多任务多优先级控制时，利用该冗余误差向次级别任务进行投影，得到的q的差值与高一级别的角度变化相加。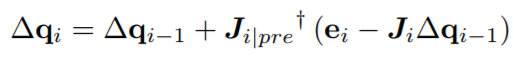
空间配置角度变化的迭代公式角度变化公式两边求导，得到角速度变化公式。 
而xi不变。
空间配置角度速度变化的迭代公式再求导得到角加速度公式，利用角加速度与MPC中得到的最优反作用力进行QP问题求解，将MPC与WBIC相结合。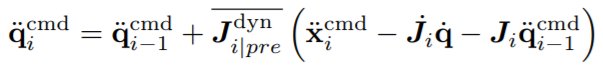
空间配置角度加速度变化的迭代公式以下是多任务控制中高低优先级任务零空间投影公式，
Jc为反作用力受力位置的连接雅克比矩阵，和文章前面的动力学公式中的Jc相同。定义迭代公式的初值：
动态Jc没有使用带+的SVD基伪逆，而是使用了动态一致性伪逆，具体原理详见高等代数。第i任务的加速命令定义如下，其中Kp和Kd分别为位置和速度的反馈增益：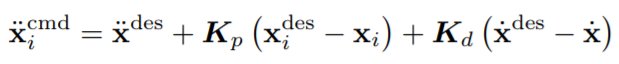
反馈增益量可否作为模型利用深度神经网络优化的切入点？最后得到：
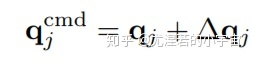通过以上公式计算得到的联合命令 
与 
被送入比例微分控制器，然后将加速度结果送到QP问题中进行优化，得出扭矩的控制命令。QP优化对加速度结果和地面反作用力进行最终的优化（到这里真的让人头秃），这里主要就是为了使用浮动基动力学模型。
标准的二次规划形式，对加速度和地面作用力进行微小的优化，并考虑连接力约束的问题。下面主要给展示一下浮动基模型化简的思路，我也没有推出最后的结果，只是觉得其主要目的是利用机器人腿部为硬性杆的条件简化复杂的浮动基公式。机器人动力学讲义中给出利用硬杆条件省略掉外部作用力的公式，仅由内部关节力矩表达，过程如下：利用腿部为硬杆得到
用第三个式子，得到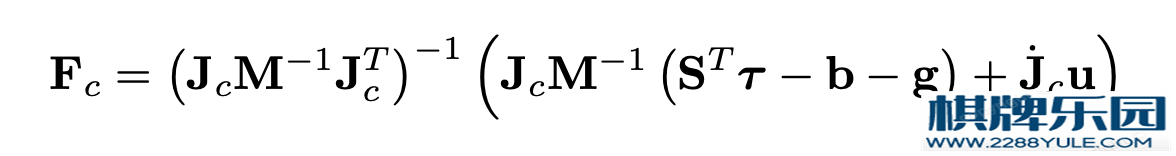
把Fc单独拿出来方便后面消去Fc定义了一个新的零空间矩阵
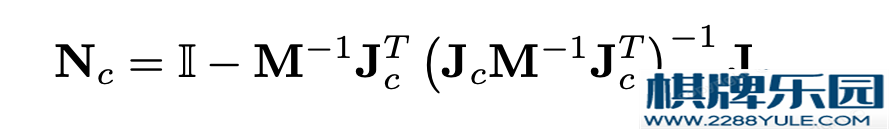得到：
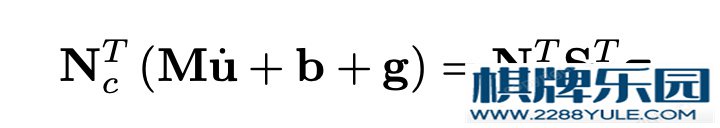我还没有仔细推过，反正讲义里省略了力矩t。在MIT论文中，思路应该是用t表达，然后消去t，得到：
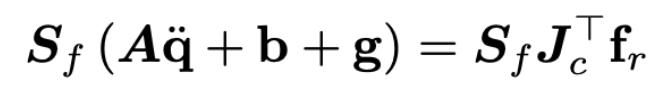总结刚考完试，回来把这个尾巴补上，很多地方都记不得了，还得重头再看一遍。后面还要看一些最新的机器人步态算法，路很漫长，最近不能光想着玩了。（2020.12.18）
麻将的较量是分轮次的较量，是有着很大程度差别的较量，而巧妙的实现对战的精彩，每个玩家都有自己可以期待的成功可能。来自于上饶麻将的基本规则当中，巧妙打法配合好，边牌的配牌胡牌的巧妙之处就更多，而玩转胡牌的时机，自然就在巧妙的配合之间，可以让游戏求得胜算的可能性，站在更自由竞技的角度，可以得到一个更好的机会来追求胜算的时机。
玩家要想上饶麻将游戏玩的好就要清楚麻将游戏的胡牌牌型都有哪些，包括平胡、七对胡、碰碰胡、十三烂、九幺、清一色、混一色等等，这些胡牌的牌点组成都是很容易记住的，玩家只要是熟悉就可以在可以胡牌的时候正确的胡牌。在游戏中，玩家要做的不仅仅是盯着自己的牌努力的胡牌，还应该盯着自己的对手出牌，如果说对手比自己胡牌早，那么赢家就是对手而不是自己，所以玩家应该尽量的阻碍对手胡牌，打出去干扰牌去迫使对手拆牌无法胡牌。
